En nuestros estudios anteriores hemos analizado movimientos unidimensionales que son aquellos que para su completo estudio sólo nos apoyamos de una coordenada. Para el caso del movimiento horizontal su posición en un momento cualquiera venía descrito por la función x(t) y esta representaba una función lineal si el movimiento era con velocidad constante o representaba una función cuadrática si el movimiento era con aceleración constante. Luego pasamos con el estudio del movimiento de caída libre y utilizábamos la coordenada y(t) para estudiar la posición del objeto durante su caída.
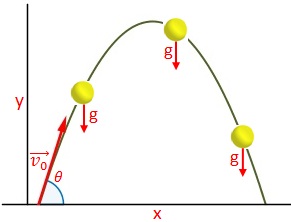
Para el estudio del movimiento parabólico nos vamos a apoyar de ambas coordenadas, esto porque es un movimiento que se da en el plano, es decir, es un movimiento bidimensional. Podemos definir de forma sencilla lo que es un movimiento parabólico de la manera siguiente: un movimiento parabólico es aquel que describe una trayectoria parabólica, por tanto, su posición durante ascenso y descenso estará descrita por una ecuación cuadrática. El movimiento parabólico al ser bidimensional, está constituido o formado por dos movimientos, sobre el eje y lo compone un movimiento rectilíneo uniformemente variado y sobre el eje x un movimiento rectilíneo uniforme. Por tanto, la posición sobre el eje x del objeto, vienen dada por una función x(t) que es lineal. De forma gráfica podemos observar que:
Esta forma geométrica se debe a que el objeto está en presencia de un campo gravitatorio uniforme. El movimiento parabólico tiene las siguientes característica:
Para el estudio del movimiento parabólico nos vamos a apoyar de ambas coordenadas, esto porque es un movimiento que se da en el plano, es decir, es un movimiento bidimensional. Podemos definir de forma sencilla lo que es un movimiento parabólico de la manera siguiente: un movimiento parabólico es aquel que describe una trayectoria parabólica, por tanto, su posición durante ascenso y descenso estará descrita por una ecuación cuadrática. El movimiento parabólico al ser bidimensional, está constituido o formado por dos movimientos, sobre el eje y lo compone un movimiento rectilíneo uniformemente variado y sobre el eje x un movimiento rectilíneo uniforme. Por tanto, la posición sobre el eje x del objeto, vienen dada por una función x(t) que es lineal. De forma gráfica podemos observar que:
Esta forma geométrica se debe a que el objeto está en presencia de un campo gravitatorio uniforme. El movimiento parabólico tiene las siguientes característica:
1. Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
2. Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales).
3. La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
4. Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
5. Se puede analizar el movimiento en vertical independientemente del horizontal.
Las ecuaciones del movimiento parabólico son básicamente 3, una que describe la posición en el eje x, otra la posición en el eje y, y una última que describe la velocidad sobre este eje.
$$y=y_{o}+v_{o}sen\theta \cdot t-\frac{1}{2}gt^{2}$$
$$x=x_{o}+v_{o}cos\theta \cdot t$$
$$v_{y}=v_{o}sen\theta -gt$$
Como podemos observar en el esquema anterior, cuando el proyectil alcanza su altura máxima, su velocidad en y se hace cero, es decir: $v_{y}=0$. Otra cosa a tomar en cuenta son los factores $v_{o}cos\theta$ y $v_{o}sen\theta$, estos son conocidos como componentes rectangulares de la velocidad inicial, $v_{ox}$ y $v_{oy}$ respectivamente. Hay que recordar que sobre el eje x el movimiento es uniforme, por tanto su velocidad nunca cambiará, sólo en el eje y.
Otros conceptos que se introducen mientras se estudia este movimiento son: alcance máximo, altura máxima y tiempo de vuelo. Cuando hablamos de alcance máximo nos referimos a la máxima distancia horizontal recorrida, desde que el cuerpo es lanzado hasta que toca el suelo. La altura máxima ya vimos que se alcanza cuando $v_{y}=0$ y el tiempo de vuelo no es mas que la suma del tiempo de subida más el tiempo de bajada, es decir, el tiempo que el proyectil tarda en el aire.
Ejemplo 1: Un objeto es disparado desde el suelo con una velocidad inicial de $80\ m/s$ y un ángulo con la horizontal de 30º. Encuentra la velocidad del objeto al cabo de 4 s y su altura máxima.
Lo primero que tenemos que hacer es sacar los datos.
Otros conceptos que se introducen mientras se estudia este movimiento son: alcance máximo, altura máxima y tiempo de vuelo. Cuando hablamos de alcance máximo nos referimos a la máxima distancia horizontal recorrida, desde que el cuerpo es lanzado hasta que toca el suelo. La altura máxima ya vimos que se alcanza cuando $v_{y}=0$ y el tiempo de vuelo no es mas que la suma del tiempo de subida más el tiempo de bajada, es decir, el tiempo que el proyectil tarda en el aire.
Ejemplo 1: Un objeto es disparado desde el suelo con una velocidad inicial de $80\ m/s$ y un ángulo con la horizontal de 30º. Encuentra la velocidad del objeto al cabo de 4 s y su altura máxima.
Lo primero que tenemos que hacer es sacar los datos.
Datos:
$v_{o}=80\ m/s$ $\theta=30º$ $v_{y}(4\ s)=?$ $
y_{max}=?$
Fórmulas:
$y=y_{o}+v_{o}sen\theta \cdot t-\frac{1}{2}gt^{2}$ $x=x_{o}+v_{o}cos\theta \cdot t$ $v_{y}=v_{o}sen\theta -gt$
Solución:
a) $v_{y}(4\ s)=(80)sen(30º)-(9.8)(4)$
$v_{y}(4\ s)=(80)(0.5)-39.2$
$v_{y}(4\ s)=40-39.2$
$v_{y}(4\ s)=0.8\ m/s$
b) Para determinar la altura máxima, es necesario primero saber el tiempo que tarda en alcanzarla, esto se calcula haciendo $v_{y}=0$.
$0=(80)sen(30º)-(9.8)t$
$(9.8)t=40$
$t=\frac{40}{9.8}=4.08\ s$
Luego:
$y_{max}=(80)sen(30º)(4.08)-\frac{1}{2}(9.8)(4.08)^{2}$
$y_{max}=163.2-(4.9)(16.64)$
$y_{max}=81.66\ m$
Ejemplo 2: Un jugador de fútbol le pega a una pelota con un ángulo de 35º con respecto al plano horizontal imprimiéndole una velocidad de 20 m/s. Determina:
a) El tiempo que dura la pelota en el aire.
b) La altura máxima alcanzada.
c) El alcance horizontal de la pelota.
Datos:
$\theta=35º$ $v_{o}=20\ m/s$ $t_{v}=?$ $y_{máx}=?$ $x_{máx}=?$
Fórmulas:
$y=y_{o}+v_{o}sen\theta \cdot t-\frac{1}{2}gt^{2}$ $x=x_{o}+v_{o}cos\theta \cdot t$ $v_{y}=v_{o}sen\theta -gt$
Solución:
a) Recordemos que el tiempo de vuelo es la suma del tiempo de bajada y de subida, y, si la posición inicial es igual a la final, entonces el tiempo de vuelo es dos veces el tiempo de subida, es decir: $t_{v}=2t_{s}$.
a) $0=(20)sen(35º)-(9.8)t_{s}$
$9.8t_{s}=11.47$
$t_{s}=1.17\ s$
$t_{v}=2(t_{s})=2.34\ s$
b) $y_{máx}=(20)sen(35º)(1.17)-\frac{1}{2}(9.8)(1.17)^{2}$
$y_{máx}=(20)(0.5736)(1.17)-(4.9)(1.37)$
$y_{máx}=13.42-6.70$
$y_{máx}=6.72\ m$
c) Recordemos que el alcance máximo se calcula con el tiempo de vuelo, tendremos entonces:
$x_{máx}=(20)cos(35º)(2.34)$
$x_{máx}=(20)(0.8191)(2.34)$
$x_{máx}=38.33\ m$
EJERCICIOS PROPUESTOS
Fórmulas:
$y=y_{o}+v_{o}sen\theta \cdot t-\frac{1}{2}gt^{2}$ $x=x_{o}+v_{o}cos\theta \cdot t$ $v_{y}=v_{o}sen\theta -gt$
Solución:
a) $v_{y}(4\ s)=(80)sen(30º)-(9.8)(4)$
$v_{y}(4\ s)=(80)(0.5)-39.2$
$v_{y}(4\ s)=40-39.2$
$v_{y}(4\ s)=0.8\ m/s$
b) Para determinar la altura máxima, es necesario primero saber el tiempo que tarda en alcanzarla, esto se calcula haciendo $v_{y}=0$.
$0=(80)sen(30º)-(9.8)t$
$(9.8)t=40$
$t=\frac{40}{9.8}=4.08\ s$
Luego:
$y_{max}=(80)sen(30º)(4.08)-\frac{1}{2}(9.8)(4.08)^{2}$
$y_{max}=163.2-(4.9)(16.64)$
$y_{max}=81.66\ m$
Ejemplo 2: Un jugador de fútbol le pega a una pelota con un ángulo de 35º con respecto al plano horizontal imprimiéndole una velocidad de 20 m/s. Determina:
a) El tiempo que dura la pelota en el aire.
b) La altura máxima alcanzada.
c) El alcance horizontal de la pelota.
Datos:
$\theta=35º$ $v_{o}=20\ m/s$ $t_{v}=?$ $y_{máx}=?$ $x_{máx}=?$
Fórmulas:
$y=y_{o}+v_{o}sen\theta \cdot t-\frac{1}{2}gt^{2}$ $x=x_{o}+v_{o}cos\theta \cdot t$ $v_{y}=v_{o}sen\theta -gt$
Solución:
a) Recordemos que el tiempo de vuelo es la suma del tiempo de bajada y de subida, y, si la posición inicial es igual a la final, entonces el tiempo de vuelo es dos veces el tiempo de subida, es decir: $t_{v}=2t_{s}$.
a) $0=(20)sen(35º)-(9.8)t_{s}$
$9.8t_{s}=11.47$
$t_{s}=1.17\ s$
$t_{v}=2(t_{s})=2.34\ s$
b) $y_{máx}=(20)sen(35º)(1.17)-\frac{1}{2}(9.8)(1.17)^{2}$
$y_{máx}=(20)(0.5736)(1.17)-(4.9)(1.37)$
$y_{máx}=13.42-6.70$
$y_{máx}=6.72\ m$
c) Recordemos que el alcance máximo se calcula con el tiempo de vuelo, tendremos entonces:
$x_{máx}=(20)cos(35º)(2.34)$
$x_{máx}=(20)(0.8191)(2.34)$
$x_{máx}=38.33\ m$
EJERCICIOS PROPUESTOS
- Una canica que rueda con una rapidez de 20 cm/s, cae por el borde de una mesa que tiene una altura de 80 cm. a) ¿cuánto tiempo necesita para chocar contra el piso? b) ¿A qué distancia horizontal del borde de la mesa chocará la canica contra el piso? Sol. a) 0.40 s b) 8.1 cm
- Un cuerpo con rapidez inicial de 40 m/s se lanza hacia arriba desde el nivel del piso, con un ángulo de 50º con la horizontal. ¿cuánto tiempo transcurrirá antes de que el cuerpo choque contra el piso? b) ¿A qué distancia del punto de partida tocará el piso? c) ¿cuál será el ángulo con la horizontal al chocar? Sol. a) 6.3 s b) 0.16 km c) 50º
- Se lanza un cuerpo hacia abajo desde el punto más alto de un edificio de 170 m de altura, formando un ángulo de 30º con la horizontal. Su rapidez inicial es de 40 m/s. a)¿cuánto tiempo transcurrirá antes de que el cuerpo llegue al piso? b) ¿A qué distancia del pie del edificio golpeará? c) ¿cuál será el ángulo con la horizontal al cual chocará? Sol. a) 4.2 s b) 0.15 km c) -60º
- Una manguera que se encuentra tendida en el piso lanza una corriente de agua hacia arriba con un ángulo de 50º con la vertical. La rapidez del agua es de 20 m/s cuando sale de la manguera. ¿A qué altura golpeará sobre una pared que se encuentra a 8 m de distancia. Sol. 5.4 m
- Un bateador en la serie mundial conecta un cuadrangular ; la pelota es impulsada con una velocidad inicial de 40 m/s y con un ángulo de 26º sobre la horizontal. Un jardinero, que tiene un alcance de 3 m sobre el suelo, se apoya contra la pared de las gradas de sol, que está a 110 m del plato de home. La pelota estaba a 120 cm sobre el piso cuando fue bateada. ¿A qué altura por encima del guante del jardinero pasa la pelota? Sol. 6 m
- Un guardabosques con una cerbatana intenta disparar un dardo tranquilizante a un mono que cuelga de una rama. El guardabosques apunta directamente al mono sin tener en cuenta que el dardo seguirá una trayectoria parabólica y pasará, por tanto, debajo del mono. Sin embargo, éste, viendo salir el dardo de la cerbatana, se suelta de la rama y cae del árbol, esperando evitar el dardo. a) Demostrar que el dardo será alcanzado independientemente de cual sea la velocidad inicial del dardo, con tal de que ésta sea lo suficientemente grande para que el dardo recorra la distancia horizontal que hay hasta el árbol antes de dar contra el suelo. Suponer que el tiempo de reacción del mono es despreciable. b) Sea $v_{d0}$ la velocidad del dardo al salir de la cerbatana. Encuentre la velocidad del dardo relativa al mono para un tiempo arbitrario t durante el vuelo del dardo.


Comentarios
Publicar un comentario